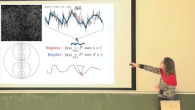
On met en branle un fluide en créant un grand tourbillon qui redistribue l'énergie qu'il a reçu à de plus petits tourbillons et ainsi de suite.
J'essaierai de vous convaincre en 5 minutes qu'il n'est pas totalement farfelu d'appeler "droite" un tripode dans le plan.
Dans cet exposé, nous verrons que l'égalité a+b=c recèle (encore) bien des mystères et que le parallèle entre nombres et polynômes est toujours féc
On dénombre des démonstrations du théorème de d'Alembert-Gauss de toute nature.
Cet exposé sera l'occasion de montrer comment les outils de développement informatique contribuent à améliorer la reproductibilité en science et co
Le modèle SIR est probablement le plus connu des modèles compartimentaux en épidémiologie.
Quand on mélange un Rubik's cube, on fait des mouvements au hasard pendant un certain temps.
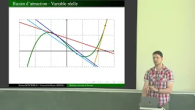
La méthode de Newton, mise au point il y a plusieurs siècles, est incontournable lorsque l'on veut approcher le zéro d'une fonction.
J'ai choisi de vous présenter ma résidence artistique au travers des deux projets que je mène conjointement.
Qui n’a jamais rêvé de faire de l’analyse sur le corps des nombres p-adiques ?
En 1902, Burnside pose la question suivante "Un groupe de type fini de torsion est-il nécessairement fini ?".
Les constructions à la règle et au compas sont fondamentales à la géométrie euclidienne du plan telle que nous la connaissons.
Divers travaux de recherche ont montré que, sans en avoir conscience, les enseignant-es peuvent contribuer à renforcer des inégalités entre les sex
Petite introduction mathématique à la théorie de la relativité restreinte ainsi qu'à certaines de ses conséquences (contraction des longueurs, "par
Née dans les années 70, puis largement popularisée dans la communauté physicienne au cours des années 80/90, la théorie de la décohérence est possi
On va expliquer pourquoi les électrons (de charge électrique négative) ne s'effondrent pas sur les noyaux (de charge électrique positive).
D'où viennent les statistiques ? À quoi et à qui servent-elles ? Avons-nous raison de penser qu'on peut "faire tout dire aux chiffres" ?
L'année 2022 a vu émerger la question des mathématiques au lycée dans le débat public au travers des médias et de la campagne présidentielle.
Quels polygones permettent de paver le plan ? La classification des polygones qui peuvent paver le plan s'est achevé en 2017 (enfin, on l'espère).
Considérons le polynôme f(z)=z^2. Le point z=0 est un point fixe attractif.
Toute communication sur un canal de propagation (radio, fibre optique, etc.) est susceptible d'être perturbée, ce qui peut conduire à des erreurs
On montrera sur un modèle simple comment se traduit en mécanique quantique la notion de transport adiabatique
Avec pour motivation l'étude de l'équidécomposabilité des polyèdres, nous discutons la rationalité d'une famille de rapports d'angles.
On expliquera comment la considération d'un groupe non abélien, en l’occurrence le groupe de Heisenberg, permet d'éclairer quelques résultats ...
Les courbes elliptiques et leur utilisation pour la signature électronique.
Théorème de réciprocité quadratique : si belle et si mystérieuse.
La compression efficace des données (notamment image et audio) est un sujet de plus en plus important depuis l’ère d’internet.
Considérons une population et un ensemble d’individus choisis au hasard dans cette population.
C'est l'une des questions classiques posées aux économistes : "Comment crée-t-on de la richesse économique ?".
On présente une bijection entre certains diagrammes de Young et des chemins de Dyck ...